Изучена температурная зависимость теплоемкости Ср ванадоцена в области 4-300К (рис. 1). Погрешность измерений Ср была такой же, как при изучении Mg(C5H5)2. Образец V(C5H5)2 очищался многократной сублимацией в вакууме (~1 Па). По данным масс-спектрометрического анализа он содержал не более 0,2 % мол. примесей (основная примесь C5H5VC5H4CH3).
На кривой Ср = f(T) ванадоцена имеется «горб »в интервале 120-200К, характерный для переходов типа «порядок - беспорядок». Отклонение теплоемкости от «нормального »хода кривой в этом интервале составляет около 5%. Обнаружена также аномалия в области 4-17К с максимумом Ср при 7,5К. В этом же интервале температуры обнаружен антиферромагнитный переход с точкой Нееля при 13,3К. Очевидно, этот переход и проявляется на кривой температурной зависимости теплоемкости.
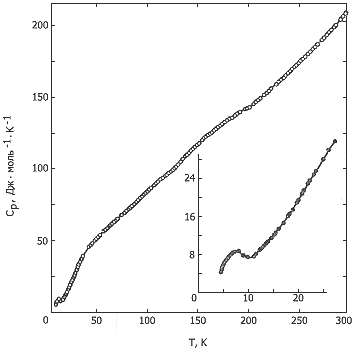
Рис. 1. Температурная зависимость теплоемкости
дициклопентадиенилванадия
По площадям, заключенным между экспериментальными кривыми Cp = f(T), а также Cp = f(lnT) (с переходами) и соответствующими интерполяционными кривыми без переходов рассчитаны энтальпии и энтропии переходов в кристаллах ванадоцена (табл. 1).
Таблица 1
Термодинамические характеристики переходов в твердом состоянии дициклопентадиенилванадия
Интервал
перехода, K |
Ttr, K |
ΔtrH,
Дж·моль-1 |
ΔtrS,
Дж·моль-1·K-1 |
| 4–17 |
7,5 |
46 ± 5 |
6,3 ± 0,6 |
| 120–200 |
|
196 ± 2 |
1,21 ± 0,01 |
Экстраполяция экспериментальных значений теплоемкости ванадоцена от 17К к 0К проведена по уравнению Ср = 2D(Θ/T). Характеристическая температура Дебая Θ = 97,2 ± 0,5К определена по экспериментальным значениям Cp в области 17-21К. В области 100-200К «нормальные» величины Cp получены графической интерполяцией участков усредняющих кривых температурной зависимости теплоемкости до и после перехода.
Численным интегрированием зависимостей Cp = f(T) и Cp = f(lnT) рассчитаны термодинамические функции ванадоцена в области 0-300К (табл. 2). Необходимые при расчете значения Cp при температуре ниже 4К получены экстраполяцией экспериментальной кривой Cp = f(T) к 0К. Погрешность значений функций при 298,15К составляет не более 0,3%.
Измерено давление пара ванадоцена эффузионным методом Кнудсена в интервале 323-338К. Полученные данные описываются уравнением: lgP(Па) = 8,92 - 3000/T, откуда энтальпия сублимации ΔsH(T) = 58,6 ± 4,2 кДж·моль-1. Эта величина пересчитана к 298,15К, при этом использовали значение ΔsCp = C(г) - Cp(к) = -41,8 Дж·моль-1К-1. Получена величина ΔsH(298,15) = 59,9 ± 4,2 кДж·моль-1. Эти данные позволили рассчитать стандартную энтропию ванадоцена в газовом состоянии S°(298,15; г) = 324,0 ± 14,1 Дж·моль-1К-1.
Таблица 2
Теплоемкость и термодинамические функции дициклопентадиенилванадия
| T, K |
Cp,
Дж·моль-1·K-1 |
H°(T)–H°(0),
кДж·моль-1 |
S°(T),
Дж·моль-1·K-1 |
-[G°(T)–H°(0)],
кДж·моль-1 |
| 5 |
6,276 |
0,005516 |
1,247 |
0,000719 |
| 50 |
53,43 |
1,307 |
48,45 |
1,115 |
| 100 |
85,06 |
4,809 |
95,19 |
4,710 |
| 140 |
110,2 |
8,691 |
127,6 |
9,173 |
| 200 |
141,5 |
16,34 |
172,7 |
18,20 |
| 240 |
164,5 |
22,44 |
200,6 |
25,68 |
| 298,15 |
204,3 |
33,12 |
240,2 |
38,48 |
В таблице 3 приведены результаты расчета энтропии и функции Гиббса образования V(C5H5)2 в конденсированном и газовом состоянии. При расчете использованы данные об энтропии соответствующих простых веществ и энтальпии образования ванадоцена.
Таблица 3
Энтропия и функция Гиббса образования дициклопентадиенилванадия
-ΔfS°(298,15; к),
Дж·моль-1K-1 |
-ΔfS°(298,15; г),
Дж·моль-1K-1 |
-ΔfG°(298,15; к),
кДж·моль-1 |
-ΔfG°(298,15; г),
кДж·моль-1 |
| 498,7 ± 1,5 |
415,0 ± 14,2 |
291,0 ± 8,4 |
326,0 ± 10,3 |
|